【学习笔记】最短路计数
前言
在补一些之前写了没A的题目的时候遇到了逛公园这题
然后这位大佬的题解又让我再次看到了我之前写过的
和没写过的
我本以为P1608路径统计是一道和最短路计数一样的水题,但是在遇到一些问题,进行一些思考之后,我发现我对最短路算法spfa和dijkstra的应用更加熟悉了一点点
我个人认为这篇文章对像我一样以前只会简单码spfa和dijkstra的同学将会有所裨益QAQ
我的思考过程
本文将向您展现我对这两题的一个思考过程,如果您对这两题的写法不是很清楚,可以参考我的思考过程
如果有哪些部分有误,还请与我私信联系QAQ但是我马上就退役了,联系肯定是假的qwq
P1144最短路计数这题我的写法是spfa
for(int i=1;i<=n;i++) dist[i]=2000001;
dist[1]=0;v[1]=1;ans[1]=1;
queue<int> q;
q.push(1);
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=h[x];i;i=e[i].nxt)
{
int y=e[i].v;
if(dist[y]>dist[x]+1)
{
dist[y]=dist[x]+1;
ans[y]=ans[x];
if(!v[y])
{
v[y]=1;
q.push(y);
}
}
else if(dist[y]==dist[x]+1)
{
ans[y]=(ans[y]+ans[x])%100003;
if(!v[y])
{
v[y]=1;
q.push(y);
}
}
}
v[x]=0;
}
也就是在处理spfa的时候当能够松弛(dist[y]>dist[x]+1)时,直接将ans[y]覆盖为ans[x],而相等时将到x最短路条数累加到y
由于spfa是广搜(但是也有在差分约束里判负环写dfs的spfa更快的,在这里不讨论,您可以自行思考),这题给的无权图相当于边权为1,注意,此时如果把搜索的顺序编为树,那么树的深度即为距离
比如
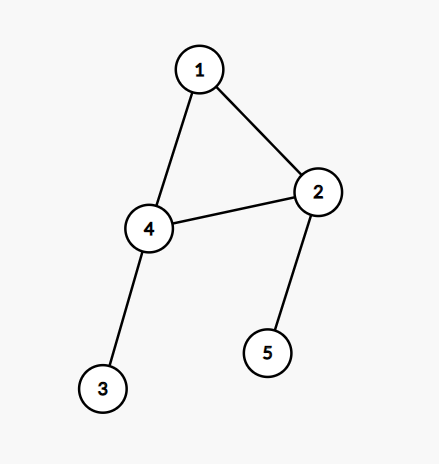
对于上面这幅图跑上面的算法搜索顺序(或者说更新顺序)是
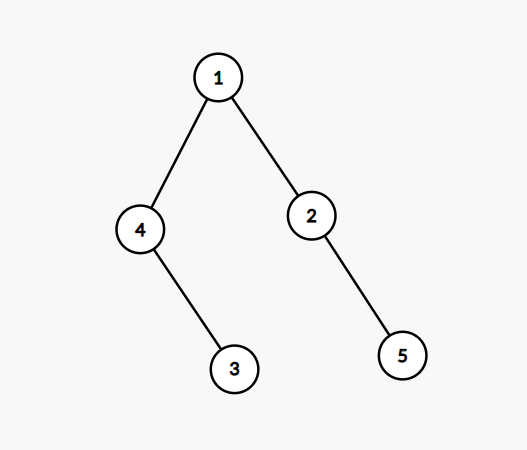
所以在搜索4连到的点的时候,4的ans已经固定不会再改了(思考一下为什么)
当您搜完4所连点(我习惯叫做“扩展4”)之后,什么情况会再搜到4?
就是队列中在4后面的某一个点x有连向4的边,但是这个点x的深度/距离一定会大于等于4的深度/距离(spfa是广搜啊QAQ),因此x在搜到4时不会更新4的ans,更没有能力将4再次加入队列
同时您也会发现,当dist[y]==dist[x]+1时,我们可以不考虑再把y加入队列的事(删掉也能过)
因为此时肯定是队列中在x前的,与x深度相同的某一点x’也连到了y,将dist[y]=dist[x’]+1,这时候已经把y加入了队列里面,并且一定是在把这些深度为dist[y]-1的点都搜完了,把其中能连到y的点的答案累加到y之后才会扩展y
可惜的是我之前并没有这样思考,只是以为这题很水
直到我用同样的写法想AP1608路径统计
我错了
而其中的关键就在于,路径统计这题是有边权的
为什么?为什么有边权就会有问题?请思考一下。。。
因为如果您写的是spfa,边权影响了您的更新顺序
测试点1就是一个很好的例子
5 5
1 2 1
2 3 1
3 4 1
1 4 3
4 5 1
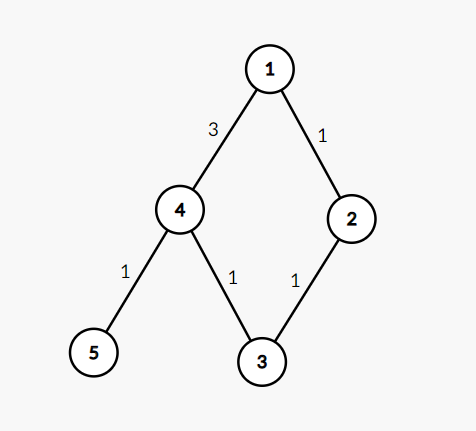
您会发现如果您这样写
while(!q.empty())
{
int x=q.front();q.pop();v[x]=0;
for(int i=h[x];i;i=e[i].nxt)
{
int y=e[i].v;
if(dis[y]==1ll*dis[x]+e[i].w)
{
ans[y]+=ans[x];
if(!v[y])
q.push(y),v[y]=1;
}
if(dis[y]>1ll*dis[x]+e[i].w)
{
dis[y]=dis[x]+e[i].w;
ans[y]=ans[x];
if(!v[y])
q.push(y),v[y]=1;
}
}
}
输出的答案为4 3
而这样写
while(!q.empty())
{
int x=q.front();q.pop();v[x]=0;
for(int i=h[x];i;i=e[i].nxt)
{
int y=e[i].v;
if(dis[y]==1ll*dis[x]+e[i].w)
{
ans[y]+=ans[x];
//if(!v[y])
//q.push(y),v[y]=1;
}
if(dis[y]>1ll*dis[x]+e[i].w)
{
dis[y]=dis[x]+e[i].w;
ans[y]=ans[x];
if(!v[y])
q.push(y),v[y]=1;
}
}
}
输出答案为4 1
对于4 3,是因为流程是
扩展1:搜到2,4,dis[2]=1,ans[2]=1,dis[4]=3,ans[4]=1
扩展2:搜到3,dis[3]=2,ans[3]=ans[2]=1
扩展4:搜到5,dis[5]=4,ans[5]=1
扩展3:搜到4,ans[4]=1
扩展4:搜到5,ans[5]+=ans[4]=3
对于4 1,是因为流程是
扩展1:搜到2,4,dis[2]=1,ans[2]=1,dis[4]=3,ans[4]=1
扩展2:搜到3,dis[3]=2,ans[3]=ans[2]=1
扩展4:搜到5,dis[5]=4,ans[5]=1
扩展3:搜到4,ans[4]=1
您会发现对于搜到了一个dis[y]==dis[x]+e[i].w的点y,您选择把它重新加入队列可能会造成答案重复,不加则可能会造成答案缺失
欸这个和刚刚说好的不一样啊
不一样的是树的深度不一定就是距离
这也就是:可能有一个深度大于x的点z,在扩展完x后,再次更新x
的ans,而此时x加入队列则会重复计数,不加入则会少计数
造成这样的结果是因为有边权
那我们怎么处理?
您注意到可能造成重复计算的是:扩展完x后有z使得x的答案被更新,此时我们需要再次更新x,但是又不能把上次扩展x时传出的答案再传一次
于是您可以选择:在上次扩展完x后把ans[x]清零
这样就能把这个问题解决了(但是不要像我这个傻逼一样把n点的答案也清零了)
while(!q.empty())
{
int x=q.front();q.pop();v[x]=0;
for(int y=1;y<=n;y++)
{
if(g[x][y]==g[0][0]) continue;
if(dis[y]==1ll*dis[x]+g[x][y])
{
ans[y]+=ans[x];
if(!v[y])
q.push(y),v[y]=1;
}
if(dis[y]>1ll*dis[x]+g[x][y])
{
dis[y]=dis[x]+g[x][y];
ans[y]=ans[x];
if(!v[y])
q.push(y),v[y]=1;
}
}
if(x!=n) ans[x]=0;
}
看似我们已经把这个问题解决了
但是我们再次思考一下,对于有权的图,我们难道不能做到在扩展x时保证x的ans不会再更新了吗?我们是学过这样的写法的!
在您翻阅题解之后会发现
为什么用dijkstra的根本没有考虑答案重复统计或者少统计的情况,就是因为dijkstra的贪心扩展过程保证了在扩展x时,x的ans不会再更新
好的,所以我们如果对dijsktra的理解度较高就可以想到用它来避免这个问题,而且根据spfa这种对一个点可能会重复搜几遍这种易被卡的性质,用dijkstra还是比较好
(说句题外话,我其实很希望有哪位大佬像写这题dijsktra可以避开spfa的问题一样,出一道题目卡一下dijsktra,当然除了负权边卡;不然我所知道的spfa的意义好像就只有跑负权图,找负权环了。。)
看似我们已经把这个问题解决了
但是我们还可以再瞄一眼边的范围
1~10?
反正我心动了
我们可以先用邻接矩阵存边,然后再用邻接表再建一次边,第二次建边时把x->y长度为c的边建成x->(cnt+1)->(cnt+2)->(cnt+c-1)->y并且每条边长度为1,然后就可以和P1144最短路计数一样的写法了
本人太菜QAQ,如果有错误请指出哦QAQ
2019.4.28