前言
虽然已经发布了讨论
但是想了想还是写一篇题解尝试让更多人发现这个问题
(其实在高赞题解的讨论中已经有人指出这个问题,但是好像没人发题解指出,我觉得我还是在退役前多发光发热QAQ)
正文
我是一只即将退役的蒟蒻QAQ
我在退役前发现了我可以hack我自己QAQ
我还发现这题的题解中可能大部分拓扑排序的写法都会被以下数据hack(为了装逼qwq重点提一下还能把第一篇目前139赞的题解中的第一种含拓扑排序的写法hack哦qwq)
4
6 7 9 1234
1 2 1
2 4 9
4 5 0
5 4 0
5 3 1
3 6 1
2 3 0
5 7 10 10000000
1 5 2
1 2 10000
1 3 10000
3 4 0
4 2 0
2 3 0
3 5 10000
8 8 0 10
1 2 1
2 3 0
3 4 0
4 8 1
5 2 0
6 5 0
7 6 0
5 7 0
8 8 0 10
1 2 1
2 3 0
3 4 0
4 8 1
2 5 0
6 5 0
7 6 0
5 7 0
第二组来源于lleo
后两组是我这个小蒟蒻的QAQ
为了大家更方便思考问题
我给出以上数据的图
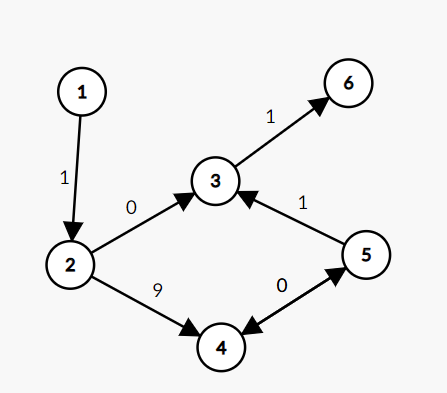
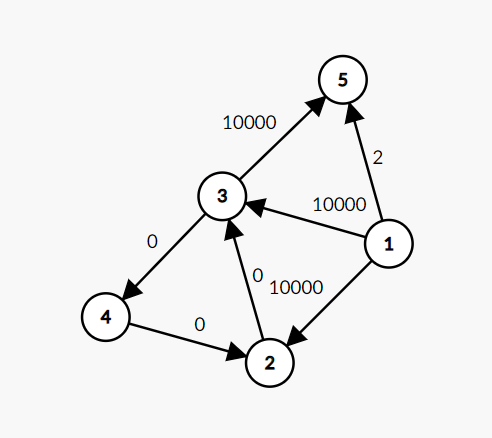
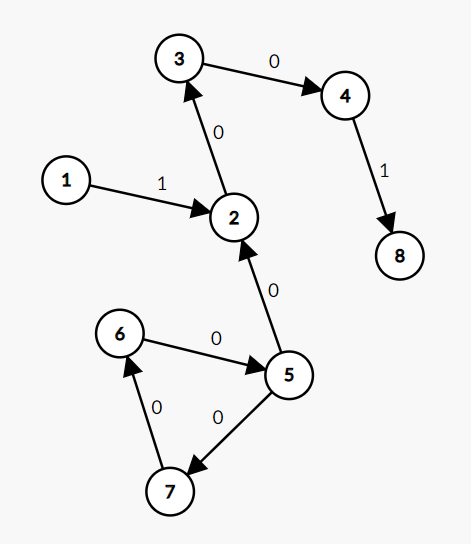
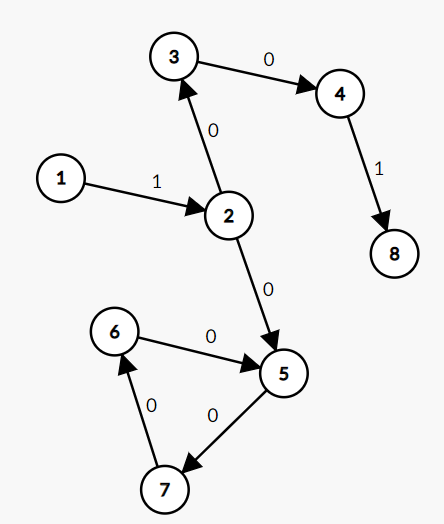
这些的正确输出应该都是1,而有些题解输出-1
我对这个错误的分析是(我一开始也错了)
1.没过第1、2个数据是没有判断0环在不在可行路径中就直接输出-1
2.直接按所有0边的图拓扑排序会造成非0环上的点被当作0环上的点
什么意思呢?
请看第三幅图
如果仅仅是按0边建,您会发现入度为0的点是没有的,也就是5,6,7,2,3,4全在0环上?显然不是
注意!拓扑排序后剩下的不仅仅是0环,还有0环连出去的路径,所以您需要怎么做?
思考一下。。。
除了对所有0边建图跑拓扑排序,您可以对所有0边反向建,再跑拓扑排序
那么这时正图入度不为0且反图入度不为0的点才真的在0环上
那么我的代码是
#include<bits/stdc++.h>
using namespace std;
const int N=100005;
const int M=200005;
int n,m,k,p;
struct Edge
{
int sum,h[N];
int v[M],w[M],nxt[M];
void adde(int x,int y,int z)
{
sum++;
v[sum]=y;
w[sum]=z;
nxt[sum]=h[x];
h[x]=sum;
}
void clear()
{
sum=0;
memset(h,0,sizeof(h));memset(v,0,sizeof(v));
memset(w,0,sizeof(w));memset(nxt,0,sizeof(nxt));
}
}e,e0,une,une0;
struct node
{
int pos,dis;int r;
node(int x=0,int y=0):pos(x),dis(y){}
friend bool operator <(node a,node b){return a.dis>b.dis;}
} g[N];
bool cmp(node a,node b){return a.dis!=b.dis?(a.dis<b.dis):(a.r<b.r);}
bool v[N];
priority_queue<node> q;
void dijkstra1()
{
for(int i=1;i<=n;i++) g[i].pos=i,g[i].dis=0x7fffffff;
memset(v,0,sizeof(v));
g[1].dis=0;
q.push(node(1,0));
while(!q.empty())
{
int x=q.top().pos;q.pop();
if(v[x]) continue;
v[x]=1;
for(int i=e.h[x];i;i=e.nxt[i])
{
int y=e.v[i];
if(g[y].dis>1ll*g[x].dis+e.w[i])
{
g[y].dis=g[x].dis+e.w[i];
q.push(node(y,g[y].dis));
}
}
}
}
int undis[N];
void dijkstra2()
{
memset(undis,127,sizeof(undis));
memset(v,0,sizeof(v));
undis[n]=0;
q.push(node(n,0));
while(!q.empty())
{
int x=q.top().pos;q.pop();
if(v[x]) continue;
v[x]=1;
for(int i=une.h[x];i;i=une.nxt[i])
{
int y=une.v[i];
if(undis[y]>1ll*undis[x]+une.w[i])
{
undis[y]=undis[x]+une.w[i];
q.push(node(y,undis[y]));
}
}
}
}
bool ine0[N];
int ind[N];
int unind[N];
void topo1()
{
int cnt=0;
queue<int> q;
for(int i=1;i<=n;i++)
if(ine0[i]&&ind[i]==0)
g[i].r=++cnt,q.push(i);
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=e0.h[x];i;i=e0.nxt[i])
{
int y=e0.v[i];
ind[y]--;
if(ind[y]==0)
g[y].r=++cnt,q.push(y);
}
}
}
void topo2()
{
int cnt=N;
queue<int> q;
for(int i=1;i<=n;i++)
if(ine0[i]&&unind[i]==0)
g[i].r=--cnt,q.push(i);
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=une0.h[x];i;i=une0.nxt[i])
{
int y=une0.v[i];
unind[y]--;
if(unind[y]==0)
g[y].r=--cnt,q.push(y);
}
}
}
int f[55][N];
int pos[N];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
e.clear();e0.clear();une.clear();une0.clear();
memset(ine0,0,sizeof(ine0));
memset(ind,0,sizeof(ind));
memset(unind,0,sizeof(unind));
scanf("%d%d%d%d",&n,&m,&k,&p);
int a,b,c;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a,&b,&c);
e.adde(a,b,c);
une.adde(b,a,c);
if(c==0)
{
ine0[a]=ine0[b]=1;
ind[b]++;unind[a]++;
e0.adde(a,b,c);une0.adde(b,a,c);
}
}
dijkstra1();
dijkstra2();
topo1();
topo2();
bool ok=0;
for(int i=1;i<=n;i++)
if(ind[i]&&unind[i]&&1ll*g[i].dis+undis[i]<=1ll*g[n].dis+k)//g[i].dis+undis[i]+k<=g[n].dis
{ok=1;break;}
if(ok){printf("-1\n");continue;}
sort(g+1,g+n+1,cmp);
for(int i=1;i<=n;i++) pos[g[i].pos]=i;
memset(f,0,sizeof(f));
f[0][pos[1]]=1;
for(int more=0;more<=k;more++)
{
for(int x=1;x<=n;x++)
{
if(f[more][x]==0) continue;
for(int i=e.h[g[x].pos];i;i=e.nxt[i])
{
int y=e.v[i];
int tmp=g[x].dis+more+e.w[i]-g[pos[y]].dis;
if(tmp<=k)
{
f[tmp][pos[y]]+=f[more][x];
while(f[tmp][pos[y]]>=p) f[tmp][pos[y]]-=p;
}
}
}
}
int ans=0;
for(int i=0;i<=k;i++) ans=(ans+f[i][pos[n]])%p;
printf("%d\n",ans);
}
return 0;
}
如果您发现您的数据可以hack我,请尽快把我叉掉,不要让我误导他人qwq
后言
我在进行了一些测试后发现目前(2019.4.29)的拓扑排序题解中只有这个和这个可以过这组数据
我太菜了好像并不能看懂第一篇分层图的写法(我不会分层图qwq)
但是第二篇我大概明白了意思,它能够过这个数据是因为它是先找出可行路径,再在可行路径上用拓扑排序判断有没有0环;而我是先用拓扑排序,在看拓扑排序后的0环在不在可行路径上(请您思考我这样讲有没有问题,我能力有限,暂时不能发现其中是否有问题)
那么总的来说还是要对于每种解法有自己的思考,不能尽信,这句话与您共勉(共勉个鬼嘞我退役了QAQ)
本人太菜QAQ,如果有错误请指出哦QAQ
2019.4.29