5.函数和代码复用
5.1 函数的定义与使用
函数的理解和定义
-
函数的定义
-
函数是一段代码的表示
- 函数是一段具有特定功能的、可重用的语句组
- 函数是一种功能的抽象,一般函数表达特定功能
- 两个作用:降低编程难度和代码复用
- 通过函数将一部分需要实现的内容/功能割离出去
def <函数名>(<参数(0个或多个)>):
<函数体>
return <返回值>
-
案例:计算n!
def fact(n): s=1 for i in range(1,n+1): s*=i return s -
y=f(x)
- 函数定义时,所指定的参数是一种占位符
- 函数定义后,如果不经过调用,不会被执行
- 函数定义时,参数是输入、函数体是处理、结果是输出(IPO)
-
函数的使用及调用过程
-
函数的调用
-
调用是运行函数代码的方式
-
调用时要给出实际参数
-
实际参数替换定义中的参数
-
函数调用后得到返回值
-
例子:用fact(10)计算10!
def fact(n): s=1 for i in range(1,n+1): s*=i return s a=fact(10) print(a)
-
-
函数的参数传递
-
参数个数
-
函数可以有参数,也可以没有,但必须保留括号
def <函数名>():
<函数体>
return <返回值>
例子:
def fact(): print("我也是函数") -
函数定义时可以为某些参数指定默认值,构成可选参数
def <函数名>(<非可选参数>,<可选参数>):#注意两者先后
<函数体>
return <返回值>
-
计算n!//m
def fact(n,m=1):#这里的m是可选参数,在使用时不给定m,则默认为1 s=1 for i in range(1,n+1): s*=i return s//m #10!==fact(10) #10!//5==fact(10,5)
-
-
可变参数传递
-
函数定义时可以设计可变数量参数,即不确定参数总数量
def <函数名>(<参数>,\*b):#\*b中的b是一个可自定义的变量名
<函数体>
return <返回值>
-
计算n!乘一些数
def fact(n,*b): s=1 for i in range(1,n+1): s*=i for item in b: s*=item return s #10!*3==fact(10,3) #10!*3*5*8==fact(10,3,5,8)像max(),min()两个函数就用了可变参数传递的方式进行定义
-
-
参数传递的两种方式
-
函数调用时,参数可以按照位置或名称方式传递
def fact(n,m=1): s=1 for i in range(1,n+1): s*=i return s//m #>>>fact(10,5)进行位置传递 #>>>fact(m=5,n=10)进行名称传递
-
函数的返回值
-
函数的返回值
-
函数可以返回0个或多个结果
-
return保留字用来传递返回值
-
函数可以有返回值,也可以没有,可以有return,也可以没有
-
return可以传递0个返回值,也可以传递任意多个返回值
def fact(n,m=1): s=1 for i in range(1,n+1): s*=i return s//m,n,m #>>>fact(10,5) #(725760,10,5) #以上用小括号,中间用逗号分隔的形式为**元组类型** #用方括号,逗号分隔的是列表类型 #两者很相似 #>>>a,b,c=fact(10,5) #>>>print(a,b,c) 725760 10 5
-
-
局部变量和全局变量
-
局部变量和全局变量
<语句块1> def <函数名>(<参数>): <函数体> return <返回值> <语句块2> 整段程序中定义的是全局变量,在函数体中定义的是局部变量 ```python n,s=10,100#n和s是全局变量 def fact(n):#fact()中的n和s是局部变量 s=1 for i in range(1,n+1): s*=i return s print(fact(n),s)#n和s是全局变量 ``` - 规则1:局部变量和全局变量是不同变量 - 局部变量是函数内部的占位符,**与全局变量可能重名但不同** - 函数运算结束后,局部变量被释放 - 可以使用global保留字在函数内部使用全局变量 ```python n,s=10,100 def fact(n):#fact()中s是局部变量与全局变量s不同 s=1 for i in range(1,n+1): s*=i return s#此处局部变量s是3628800 print(fact(n),s)#此处全局变量s是100 #运行结果 #3628800 100 --- n,s=10,100 def fact(n): global s#fact()中使用global保留字声明此处s是全局变量s for i in range(1,n+1): s*=i return s#此处s指全局变量s print(fact(n),s)#此处全局变量s被函数修改 #运行结果 #362880000 362880000 ``` - 规则2:局部变量为**组合数据类型且并未创建**,等同于局部变量 ```python ls=["F","f"]#通过使用[]真实创建了一个全局变量列表ls def func(a): ls.append(a)#此处ls是列表类型,未真实创建 则等同于全局变量 return func("C")#全局变量ls被修改 print(ls) #运行结果 #['F','f','C'] --- ls=["F","f"]#通过使用[]真实创建了一个全局变量列表ls def func(a): ls=[] ls.append(a)#此处ls是列表类型,真实创建 是局部变量 return func("C")#局部变量ls被修改 print(ls) #运行结果 #['F','f'] ``` 具体解释:组合数据类型在python中由指针来体现,函数中如果没真实创建组合数据类型,它使用的变量是指针,而指针指向外部的全局变量,所以修改这个指针对应的内容则修改的是全局变量 - 使用规则 - 基本数据类型,无论是否重名,局部变量与全局变量不同 - 可以通过global保留字在函数内部声明全局变量 - 组合数据类型,如果局部变量**未真实创建**,则是全局变量
lambda函数
-
lambda函数
- lambda函数返回函数名作为结果
- lambda函数是一种匿名函数,即没有名字的函数
- 使用lambda保留字定义,函数名是返回结果
- lambda函数用于定义简单的、能够在一行内表示的函数
- lambda函数返回函数名作为结果
-
lambda函数的应用
- 谨慎使用lambda函数
- lambda函数主要用作一些特定函数或方法的参数
- lambda函数有一些固定使用方式,建议逐步掌握
- 一般情况,建议使用def定义的普通函数(除非知道lambda函数的固定搭配和固定使用)
- 谨慎使用lambda函数
5.2 实例7:七段数码管绘制
“七段数码管绘制”问题分析
- 七段数码管
- 选择不同数码管的亮灭可以构成不同的数字和字母组合
- 需求:用程序绘制七段数码管
- turtle绘图体系
“七段数码管绘制”实例讲解
-
基本思路
- 步骤1:绘制单个数字对应的数码管
- 步骤2:获得一串数字,绘制对应的数码管
- 步骤3:获得当前系统时间,绘制对应的数码管
-
步骤1:绘制单个数字对应的数码管
- 七段数码管由7个基本线条组成
- 七段数码管可以有固定顺序
- 不同数字显示不同线条
import turtle def drawLine(draw):#绘制单段数码管 turtle.pendown() if draw else turtle.penup() turtle.fd(40) turtle.right(90) def drawDigit(digit):#根据数字绘制七段数码管 drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False) drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,2,6,8] else drawLine(False) turtle.left(90) drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False) drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False) turtle.left(180) turtle.penup()#为绘制后续数字确定位置 turtle.fd(20)#为绘制后续数字确定位置 -
步骤2:获取一段数字,绘制多个数码管
import turtle def drawLine(draw):#绘制单段数码管 turtle.pendown() if draw else turtle.penup() turtle.fd(40) turtle.right(90) def drawDigit(digit):#根据数字绘制七段数码管 drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False) drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,2,6,8] else drawLine(False) turtle.left(90) drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False) drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False) turtle.left(180) turtle.penup()#为绘制后续数字确定位置 turtle.fd(20)#为绘制后续数字确定位置 def drawDate(date):#获得要输出的数字 for i in date: drawDigit(eval(i))#通过eval()函数将数字变为整数 def main(): turtle.setup(800,350,200,200) turtle.penup() turtle.fd(-300) turtle.pensize(5) drawDate('20181010') turtle.hideturtle()#藏起海龟 turtle.done() main()推荐先复制粘贴上面的代码,运行后再尝试理解每段代码的作用
-
步骤3:获得当前系统时间,绘制对应的数码管
在此之前,让我们尝试绘制漂亮的七段数码管(增加drawGap函数)
import turtle def drawGap():#绘制数码间隔 turtle.penup() turtle.fd(5) def drawLine(draw):#绘制单段数码管 drawGap() turtle.pendown() if draw else turtle.penup() turtle.fd(40) drawGap() turtle.right(90) def drawDigit(digit):#根据数字绘制七段数码管 xxx xxx- 使用time库获取当前系统时间
- 增加年月日标记
- 年月日颜色不同
现在对drawDate函数的输入参数date做一个修改,date为日期,date格式规定为’%Y-%m=%d+’,将-、=、+分别对应汉字年、月、日
import turtle,time xxx def drawDate(date):#date格式为'%Y-%m=%d+' turtle.pencolor("red") for i in date: if i=='-': turtle.write('年',font=("Arial",18,"normal")) turtle.pencolor("green") turtle.fd(40) elif i=='=': turtle.write('月',font=("Arial",18,"normal")) turtle.pencolor("blue") turtle.fd(40) elif i=='+': turtle.write('日',font=("Arial",18,"normal")) else: drawDigit(eval(i)) xxx为了获得当前系统时间并将其格式化为上面需要的date形式,使用time库中的gmtime,strftime
import turtle,time xxx def main(): turtle.setup(800,350,200,200) turtle.penup() turtle.fd(-300) turtle.pensize(5) drawDate(time.strftime('%Y-%m=%d+',time.gmtime())) turtle.hideturtle() turtle.done() main()下面是整个程序的代码
import turtle,time def drawGap():#绘制数码间隔 turtle.penup() turtle.fd(5) def drawLine(draw):#绘制单段数码管 drawGap() turtle.pendown() if draw else turtle.penup() turtle.fd(40) drawGap() turtle.right(90) def drawDigit(digit):#根据数字绘制七段数码管 drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False) drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,2,6,8] else drawLine(False) turtle.left(90) drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False) drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False) drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False) turtle.left(180) turtle.penup()#为绘制后续数字确定位置 turtle.fd(20)#为绘制后续数字确定位置 def drawDate(date):#date格式为'%Y-%m=%d+' turtle.pencolor("red") for i in date: if i=='-': turtle.write('年',font=("Arial",18,"normal")) turtle.pencolor("green") turtle.fd(40) elif i=='=': turtle.write('月',font=("Arial",18,"normal")) turtle.pencolor("blue") turtle.fd(40) elif i=='+': turtle.write('日',font=("Arial",18,"normal")) else: drawDigit(eval(i)) def main(): turtle.setup(800,350,200,200) turtle.penup() turtle.fd(-300) turtle.pensize(5) drawDate(time.strftime('%Y-%m=%d+',time.gmtime())) turtle.hideturtle() turtle.done() main()
“七段数码管绘制”举一反三
- 理解方法思维
- 模块化思维:确定模块接口,封装功能
- 规则化思维:抽象过程为规则,计算机自动执行
- 化繁为简:将大功能变为小功能组合,分而治之(函数降低编码难度的主要方式)
- 应用问题的扩展
- 绘制带小数点的七段数码管
- 带刷新的时间倒计时效果
- 绘制高级的数码管,不局限于七段
5.3 代码复用与函数递归
代码复用与模块化设计
-
代码复用
-
把代码当成资源进行抽象
- 代码资源化:程序代码是一种用来表达计算的“资源”
- 代码抽象化:使用函数等方法对代码赋予更高级别的定义
- 代码复用:同一份代码在需要时可以被重复使用
-
函数和对象是代码复用的两种主要形式
-
函数:将代码命名,在代码层面建立了初步抽象
(这种抽象级别比较低,只是将代码变成了一个功能组)
-
对象:通过属性和方法,即<a>.<b>和<a>.<b>()在函数之上再次组织进行抽象
(这里不再深入介绍“对象”“面向对象编程”,只需理解函数是对代码的抽象;“再次组织的抽象”实际上是一种“面向对象的程序设计方法”)
-
-
-
模块化设计
-
分而治之
- 通过函数或对象封装将程序划分为模块及模块间的表达
- 具体包括:主程序、子程序和子程序间关系
- 分而治之:一种分而治之,分层抽象,体系化的设计思想
-
紧耦合 松耦合
-
紧耦合:两个部分之间交流很多,无法独立存在
-
松耦合:两个部分之间交流很少,可以独立存在
-
模块(函数)内部紧耦合(通过局部变量进行数据传输),模块(函数)之间松耦合(在函数之间减少传递参数和返回值)
(原因:函数的输入参数和返回值,就是这段函数与其他代码之间的交流通道,这样的交流通道越少越清晰,这段函数的复用可能性就越高)
-
-
函数递归的理解
-
递归的定义
-
函数定义中调用函数自身的方式
例子:
$n!=\begin{cases}1 \quad n=0 \ n(n-1)! \quad otherwise \end{cases}$
-
两个关键特征
-
链条:计算过程存在递归链条
n!与(n-1)!构成递归链条
-
基例:存在一个或多个不需要再次递归的基例(基础的实例)
n=0时n!=1
-
-
类似数学归纳法
- 数学归纳法
- 证明当$n$取第一个值$n_0$时命题成立
- 假设当$n_k$时命题成立,证明当$n=n_{k+1}$时命题也成立
- 递归是数学归纳法思维的编程体现
-
函数递归的调用过程
-
递归的实现
$n!=\begin{cases}1 \quad n=0 \ n(n-1)! \quad otherwise \end{cases}$
def fact(n): if n==0: return 1 else: return n*fact(n-1)- 函数+分支语句
- 递归本身是一个函数,需要函数定义方式描述
- 函数内部,采用分支语句对输入参数进行判断
- 基例和链条,分别编写对应代码
分析:上例中求fact(5)时,fact(5)->5*fact(4)->5*4*fact(3)->5*4*3*fact(2)->5*4*3*2*fact(1)->5*4*3*2*1*fact(0)->5*4*3*2*1*1->5*4*3*2*1->5*4*3*2->5*4*6->5*24->120
函数定义时调用的是自身,而执行时调用的是自身代码的不同复制版本
- 函数+分支语句
函数递归实例分析
-
字符串反转
- 将字符串s反转后输出
- 简单:s[::-1](-1的步长即反转)
- 函数+分支结构
- 确定递归链条(首字符放最后,其余字符再反转)
- 确定递归基例(空字符)
def rvs(s): if s=="": return s else: return rvs(s[1:])+s[0] -
斐波那契数列
- 一个经典数列
- $F(n)=\begin{cases}1 \quad n=1 \ 1 \quad n=2 \ F(n-1)+F(n-2) \quad otherwise \end{cases}$
- 函数+分支结构
- 递归链条(F(n)=F(n-1)+F(n-2))
- 递归基例(n=1/2)
def f(n): if n==1 or n==2: return 1 else: return f(n-1)+f(n-2) -
汉诺塔
- 汉诺塔(又称河内塔)问题源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
- 对于给定数量的圆盘,从最左侧搬运到最右侧需要多少步骤
- 该怎么搬运:既然是n个圆盘从A到C,就相当于n-1个圆盘先从A到B,再将第n个从A到C,再将n-1个从B到C(想一下,为符合规则只能这样)
- 递归过程只关心递归链条,我只要知道n到n-1怎么搬,不需要关心n-1具体怎么搬
count=0 def hanoi(n,src,dst,mid): global count if n==1: print("{}:{}->{}".format(1,src,dst)) count+=1 else: hanoi(n-1,src,mid,dst) print("{}:{}->{}".format(n,src,dst)) count+=1 hanoi(n-1,mid,dst,src) #例:hanoi(3,"A","C","B") # print(count)
5.4 模块4:PyInstaller库的使用
PyInstaller库基本介绍
- 前言
- 存在需求:将编写的.py源代码转换成无需源代码的可执行文件(如Windows下.exe)即将编好的程序发给电脑没有python环境的朋友玩
- 原因:在Windows,Linux,OS操作系统上可能有时没有安装python的解释器,此时就需要将源程序先编译、打包成一个可执行文件
- PyInstaller库概述
- 将.py源代码转换成无需源代码的可执行文件
- .py->PyInstaller->可执行文件
- PyInstaller库是第三方库
- 官方网站
- 第三方库:使用前需要额外安装
- 安装第三方库python提供了好用的pip工具
- 安装需要Windows下command命令行或者Linux或OS系统下相应命令行去执行pip指令
- PyInstaller库的安装(Windows下安装)
- Win+R打开“运行”
- 运行cmd
- (cmd命令行)pip install pyinstaller
- 需要联网安装
- 安装完后出现successfully installed则安装好
PyInstaller库使用说明
-
注意:用Windows下的命令行使用PyInstaller,因为它是命令行的执行程序,而不是python下的执行命令
-
简单的使用
- (cmd命令行)pyinstaller -F <文件名.py>
- 目录中出现额外的三个目录_pycache_,build,dist
- 其中_pycache_,build可以安全删除,dist文件夹中有打包之后生成的exe文件,可以鼠标双击执行
-
PyInstaller库常用参数
-
-h 查看帮助
-
–clean 清理打包过程中的临时文件
-
-D,–onedir 默认值,生成dist文件夹
-
-F,–onefile 在dist文件夹中只生成独立的打包文件
-
-i <图标文件名.ico> 指定打包程序使用的图标(icon)文件
如:pyinstaller -i x.ico -F y.py
-
5.5 实例8:科赫雪花小包裹
“科赫雪花小包裹”问题分析
- 科赫雪花
- 高大上的分形几何
- 分形几何是一种具有迭代关系的几何图形,广泛存在于自然界中
- 科赫曲线,也叫雪花曲线
- 高大上的分形几何
- 科赫雪花绘制
- 用Python绘制科赫曲线
- 对一段线段,取其中间1/3长度,去掉后增加两条1/3长度的线段,这样就形成一个60°的突起
- 这样一条直线到这样一种曲线的变换叫一次科赫曲线的转换
- 0阶科赫曲线是一段线段,每“对其中的每条线段做一次变化”就升一阶
- 用Python绘制科赫曲线
“科赫雪花小包裹”实例讲解
-
科赫曲线的绘制(绘制n阶科赫曲线)
- 递归思想:函数+分支
- 递归链条:线段的组合
- 递归基例:初始线段
#KochDrawV1.py import turtle def koch(size,n): if n==0: turtle.fd(size) else: for angle in [0,60,-120,60]: turtle.left(angle) koch(size/3,n-1) def main(): turtle.setup(800,400) turtle.penup() turtle.goto(-300,-50) turtle.pendown() turtle.pensize(2) koch(600,3) turtle.hideturtle() main() -
科赫曲线->科赫雪花
#KochDrawV1.py import turtle def koch(size,n): xxx def main(): turtle.setup(600,600) turtle.penup() turtle.goto(-200,100) turtle.pendown() turtle.pensize(2) level=3 koch(400,level) turtle.right(120) koch(400,level) turtle.right(120) koch(400,level) turtle.right(120) turtle.hideturtle() main() -
pyinstaller -i curve.ico -F KochDrawV1.py
“科赫雪花小包裹”举一反三
- 绘制条件的扩展
- 修改分形几何绘制阶数
- 修改科赫曲线的基本定义及旋转角度
- 修改绘制科赫雪花的基本框架图形
- 分形几何千千万
- 康托尔集、谢尔宾斯基三角形、门格海绵…
- 龙形曲线、空间填充曲线、科赫曲线…
- 深入理解函数递归思想
练习
-
实例7:七段数码管绘制
描述
这是”实例”题,与课上讲解实例相同,请作答检验学习效果。
七段数码管是一种展示数字的有效方式。
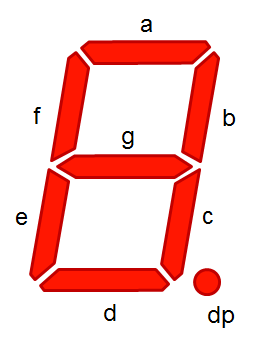

请用程序绘制当前系统时间对应的七段数码管,效果如下:

要求如下:
(1) 使用 time 库获得系统当前时间,格式如下:20190411
(2) 绘制对应的七段数码管
(3) 数码管风格不限
请在本机编写代码完成实例,建议有趣的风格请在Python123的绘图专区上传展示。
import time,turtle def drawLine(draw): turtle.penup() turtle.fd(5) turtle.pendown() if draw else turtle.penup() turtle.fd(40) turtle.penup() turtle.fd(5) turtle.right(90) def drawDigit(d): drawLine(True) if d in [2,3,4,5,6,8,9] else drawLine(False) drawLine(True) if d in [0,1,3,4,5,6,7,8,9] else drawLine(False) drawLine(True) if d in [0,2,3,5,6,8,9] else drawLine(False) drawLine(True) if d in [0,2,6,8] else drawLine(False) turtle.left(90) drawLine(True) if d in [0,4,5,6,8,9] else drawLine(False) drawLine(True) if d in [0,2,3,5,6,7,8,9] else drawLine(False) drawLine(True) if d in [0,1,2,3,4,7,8,9] else drawLine(False) turtle.left(180) turtle.penup() turtle.fd(20) def drawDate(date): turtle.pencolor("red") for i in date: drawDigit(eval(i)) def main(): turtle.setup(800,350,200,200) turtle.penup() turtle.fd(-300) turtle.pensize(5) drawDate(time.strftime('%Y%m%d',time.gmtime())) turtle.done() main() -
实例8:科赫雪花小包裹
描述
这是”实例”题,与课上讲解实例相同,请作答检验学习效果。
科赫曲线,也叫雪花曲线。绘制科赫曲线。
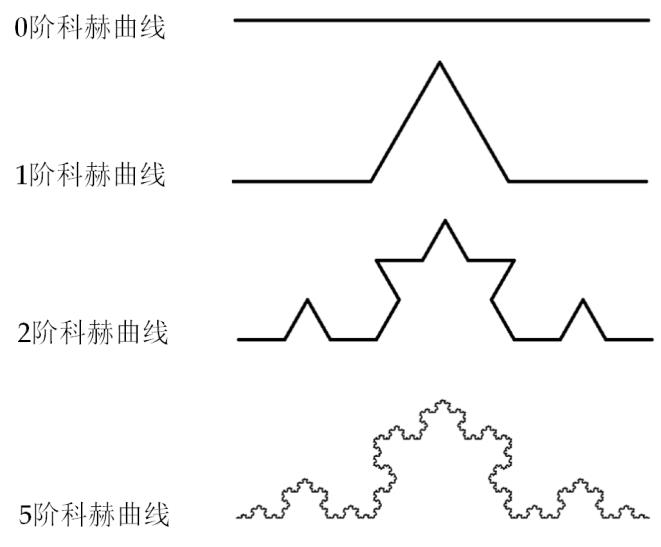
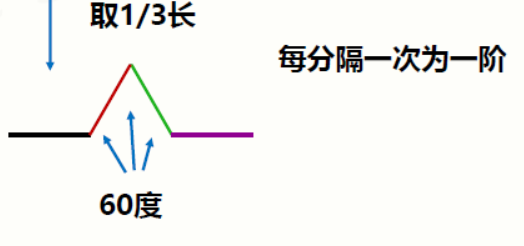
请补充编程模板中代码,完成功能:获得用户输入的整数N,作为阶,绘制N阶科赫曲线。
import turtle def koch(size, n): if n == 0: turtle.fd(size) else: for angle in [0, 60, -120, 60]: turtle.left(angle) koch(size/3, n-1) def main(level): turtle.setup(600,600) turtle.penup() turtle.goto(-200, 100) turtle.pendown() turtle.pensize(2) koch(400,level) turtle.right(120) koch(400,level) turtle.right(120) koch(400,level) turtle.hideturtle() try: level = eval(input("请输入科赫曲线的阶: ")) main(level) except: print("输入错误") -
625673
任意累积
描述
请根据编程模板补充代码,计算任意个输入数字的乘积。
注意,仅需要在标注…的地方补充一行或多行代码。
输入输出示例
输入 输出 示例 1 1,2,3,424def cmul(*num): sum=1 for i in num: sum*=i return sum print(eval("cmul({})".format(input()))) --- def cmul(a, *b): m = a for i in b: m *= i return m print(eval("cmul({})".format(input()))) -
斐波那契数列计算
描述
根据编程模板补充代码,计算斐波那契数列的值,具体功能如下:
\1. 获取用户输入整数N,其中,N为正整数
\2. 计算斐波那契数列的值
如果将斐波那契数列表示为fbi(N),对于整数N,值如下:
fbi(1)和fbi(2)的值是1,当N>2时,fbi(N) = fbi(N-1) + fbi(N-2)
请采用递归方式编写。
输入输出示例
输入 输出 示例 1 43def fbi(n): if n==1 or n==2: return 1 else: return fbi(n-1)+fbi(n-2) n=eval(input()) print(fbi(n)) -
汉诺塔实践
描述
汉诺塔问题大家都清楚,这里不再赘述。
请补充编程模板中代码,完成如下功能:
有三个圆柱A、B、C,初始时A上有N个圆盘,N由用户输入给出,最终移动到圆柱C上。
每次移动步骤的表达方式示例如下:[STEP 10] A->C。其中,STEP是步骤序号,宽度为4个字符,右对齐。
请编写代码,获得输入N后,输出汉诺塔移动的步骤。
输入格式
一个整数
输出格式
每个步骤一行,每行参考格式如下:[STEP 10] A->C
输入输出示例
输入 输出 示例 1 3[STEP 1] A->C [STEP 2] A->B [STEP 3] C->B [STEP 4] A->C [STEP 5] B->A [STEP 6] B->C [STEP 7] A->Cstep=1 def hanoi(n,a,c,b): global step if n==1: print("[STEP{:>4}] {}->{}".format(step,a,c)) step+=1 else: hanoi(n-1,a,b,c) #print("[STEP{:>4}] {}->{}".format(step,a,b)) print("[STEP{:>4}] {}->{}".format(step,a,c)) step+=1 hanoi(n-1,b,c,a) #print("[STEP{:>4}] {}->{}".format(step,b,c)) n=eval(input()) hanoi(n,'A','C','B')
测验
单项选择题
-
以下选项不是函数作用的是:
A. 提高代码执行速度
B. 降低编程复杂度
C. 增强代码可读性
D. 复用代码
A
函数不能直接提高代码执行速度。
-
下列程序的输出结果为:
def f(a,b): a=4 return a+b def main(): a=5 b=6 print(f(a,b),a+b) main()A. 11 10
B. 10 11
C. 10 10
D. 11 11
B
这里没有全局变量,都是函数局部变量的运算。
-
以下关于Python函数说法错误的是:
def func(a,b): c=a**2+b b=a return c a=10 b=100 c=func(a,b)+aA. 执行该函数后,变量a的值为10
B. 该函数名称为func
C. 执行该函数后,变量b的值为100
D. 执行该函数后,变量c的值为200
D
a, b为全局变量,请在IDLE中执行代码观察结果。
-
以下关于函数调用描述正确的是:
A. 自定义函数调用前必须定义
B. Python内置函数调用前需要引用相应的库
C. 函数在调用前不需要定义,拿来即用就好
D. 函数和调用只能发生在同一个文件中
A
函数调用前必须已经存在函数定义,否则无法执行。
Python内置函数直接使用,不需要引用任何模块。
-
以下关于模块化设计描述错误的是:
A. 应尽可能合理划分功能块,功能块内部耦合度高
B. 应尽可能合理划分功能块,功能块内部耦合度低
C. 高耦合度的特点是复用较为困难
D. 模块间关系尽可能简单,模块之间耦合度低
B
模块内高耦合、模块间低耦合。
-
以下对递归描述错误的是:
A. 一定要有基例
B. 书写简单
C. 执行效率高
D. 递归程序都可以有非递归编写方法
C
递归不提高程序执行效率。
任何递归程序都可以通过堆栈或队列变成非递归程序(这是程序的高级应用)。
-
以下关于函数说法错误的是:
A. 对函数的使用必须了解其内部实现原理
B. 函数通过函数名来调用
C. 函数是一段具有特定功能的、可重用的语句组
D. 函数可以看做是一段具有名字的子程序
A
调用函数不需要知道函数内部实现原理,只需要知道调用方法(即接口)即可。
-
哪个选项对于函数的定义是错误的?
A. def vfunc(*a,b):
B. def vfunc(a,*b):
C. def vfunc(a,b):
D. def vfunc(a,b=2):
A
def vfunc(*a, b) 是错误的定义:*a表示可变参数,可变参数只能放在函数参数的最后。
-
关于return语句,以下选项描述正确的是:
A. 函数中最多只有一个return语句
B. return只能返回一个值
C. 函数必须有一个return语句
D. 函数可以没有return语句
D
函数可以包含0个或多个return语句
-
以下关于递归函数基例的说法错误的是:
A. 每个递归函数都只能有一个基例
B. 递归函数必须有基例
C. 递归函数的基例不再进行递归
D. 递归函数的基例决定递归的深度
A
每个递归函数至少存在一个基例,但可能存在多个基例。
程序设计题
-
随机密码生成
描述
补充编程模板中代码,完成如下功能:
以整数17为随机数种子,获取用户输入整数N为长度,产生3个长度为N位的密码,密码的每位是一个数字。每个密码单独一行输出。
产生密码采用random.randint()函数。
输入输出示例
输入 输出 示例 1 3634 524 926#请在...补充代码 import random def genpwd(length): if length==1: return random.randint(0,9) else: return random.randint(10**(length-1),10**length-1) length = eval(input()) random.seed(17) for i in range(3): print(genpwd(length)) --- import random def genpwd(length): if length==1: return random.randint(0,9) else: return random.randint(10**(length-1),10**length-1) length = eval(input()) random.seed(17) for i in range(3): print(genpwd(length)) --- import random def genpwd(length): a = 10**(length-1) b = 10**length - 1 return "{}".format(random.randint(a, b)) length = eval(input()) random.seed(17) for i in range(3): print(genpwd(length)) -
连续质数计算
描述
补充编程模板中代码,完成如下功能:
获得用户输入数字N,计算并输出从N开始的5个质数,单行输出,质数间用逗号,分割。
注意:需要考虑用户输入的数字N可能是浮点数,应对输入取整数;最后一个输出后不用逗号。
输入输出示例
输入 输出 示例 1 1213,17,19,23,29# 请在...补充一行或多行代码 def prime(m): ... n = eval(input()) ... --- def prime(m): if m==2: return True else: for i in range(2,m): if m%i==0: return False return True n = eval(input()) #if round(n)<n: # n=round(n)+1#wrong->round()是四舍五入 if int(n)<n: n=int(n)+1 cnt=0 while True: if prime(n): if cnt==4: print(n,end="") break; else: print("{},".format(n),end="") cnt+=1 n+=1 --- def prime(m): for i in range(2,m): if m % i == 0: return False return True n = eval(input()) n_ = int(n) n_ = n_+1 if n_ < n else n_ count = 5 while count > 0: if prime(n_): if count > 1: print(n_, end=",") else: print(n_, end="") count -= 1 n_ += 1 这个代码注意: (1) 需要对输入小数情况进行判断,获取超过该输入的最小整数(这里没用floor()函数);#floor()似乎是math库里的 (2) 对输出格式进行判断,最后一个输出后不增加逗号(这里没用.join()方法)。